comsol 5.2破解版下载[网盘资源]-COMSOL Multiphysics 5.2中文破解版下载

comsol 5.2是由COMSOL公司推出的一款全球通用的基于高级数值方法和模拟物理场问题的通用软件，COMSOL公司是全球最知名的多物理场建模与仿真解决方案的提倡者和领导者。软件具有无与伦比的模拟和仿真能力，其集结构力学模块、化学工程模块、热传递模块等八大模块于一身。用户可通过这些模块模拟和赋予设计理念，可使所有的物理现象字计算机完美重现，并可帮助用户解释耦合现象或多物理场现象。comsol 5.2包含超过30个附加模块供用户选择。并可以通过电气、力学、流体流动和化学等领域的专用物理接口和工具，来进一步扩展该仿真平台。附加的接口模块可以将COMSOL Multiphysics仿真与技术计算、CAD和ECAD等软件相连接。新版comsol 5.2全新增加九大功能，包括多物理场、几何和网格、求解和求解器、力学和流体等。其中几何和网络，现在用户可以genuine导入的网格构建几何，并可通过链接的子序列调用几何子序列，可提升大型阵列和CAD装配体的处理速度。多物理场中全新预定义多物理场耦合包括焦耳热和热膨胀、电磁感应、微波、激光加热和热电和压电效应等。更多全新功能，用户自行进入探索吧。

comsol5.2安装教程

知识兔一、鼠标右键点击“COMSOL_5.2_DVD.iso”文件，并点击打开“解压文件”

二、双击“setup.exe”开始正式的安装
三、选择语言，支持(简体中文)，默认勾选简体中文，并点击下一步

四、点击“新安装 COMSOL 5.2”

五、勾选“我接受许可协议中的条款”，并将许可证格式修改为“许可证文件”，然后点击浏览载入安装包中“_SolidSQUAD_”目录下的“Comsol52_SSQ.lic”

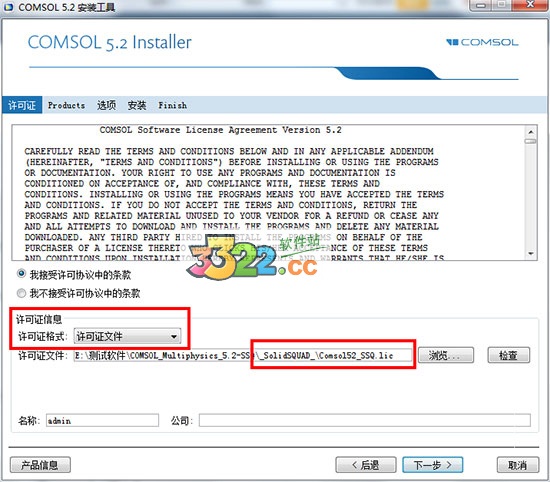
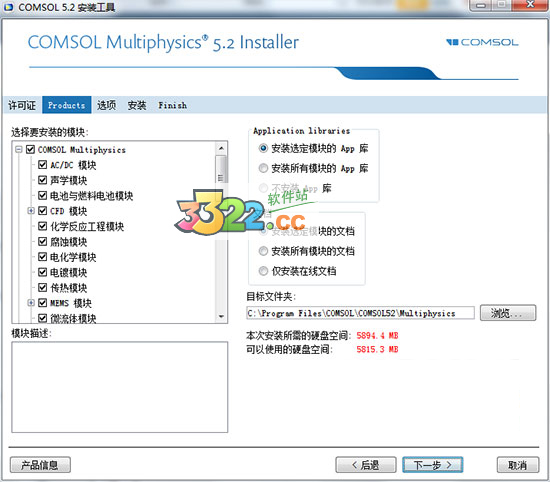
六、选择安装模块和安装目录:
1.在安装的模块可勾选
1)AC/DC模块
2)声学模块
3)电池与燃料电池模块
4)CFD模块
5)化学反应工程模块
6)腐蚀模块
7)电化学模块
8)电镀模块
9)传热模块
10)MEMS模块
11)微流体模块
2.可勾选
1)安装选定模块的APP库
2)安装所有模块的APP库
3)不安装APP库
默认勾选第一项，也建议勾选
3.文档项目，可勾选:
1)安装选定模块的文档
2)安装所有模块的文档
3)仅安装在线文档
默认勾选安装选定模块的文档，建议勾选。完成选项勾并选择安装目录，建议默认，但需要注意的是本次安装需要的硬盘空间为5894.4M

七、可以添加MATLAB、Pro/E等软件的链接，直接默认并点击下一步

八、等待安装完成，安装的时间可能过长，用户需耐心等待

九、安装中途会弹出DX的安装程序，接受协议后按照提示点击下一步
十、安装完成

十一、安装的时候载入过证书，所以直接运行桌面COMSOL 5.2的快捷方式就可以进入程序了，现在用户可直接完全免费的使用comsol5.2啦

comsol使用技巧

知识兔一、全局约束  
对于多物理仿真，添加全局约束是COMSOL非常有用的功能之一
1.例如，对于一个涉及传热的仿真，希望能够调整热源Q_0的大小，从而使得某一位置处的温度T_probe恒定在指定值T_max，知识兔可以直接将这个全局约束添加进来即可
2.有些情况下，全局约束可能包含有对时间的微分项，也就是常说的常微分方程（ODE），COMSOL同样也支持自定义ODE作为全局约束
3.例如，在一个管道内流体+物质扩散问题的仿真中，利用PID算法控制管道入口的流速u_in_ctrl，从而使得某一位置处的浓度conc恒定在指定值c_set。（基本模块模型库 > Multidisciplinary > PID control）
4.要添加上述约束，除变上限积分项外，另外两项都可以很容易的在边界条件中的“入口流速”设置中直接定义。因此，这个变上限积分需要转化成一个ODE，作为全局约束加入
5.令方程两边同对时间t求导，得到 setcconcdt d_int。在COMSOL中，变量u对时间的导数，用ut表示。因此变量int的时间导数即为intt。利用COMSOL的“ODE设定”，知识兔可以很容易的将intt-(conc-c_set)=0这个ODE全局约束添加入模型之中
二、积分耦合变量
COMSOL的语法中，变量u对空间的微分，分别默认为用ut，ux，uy，uz等来表示，这为仿真分享了极大的便利。那么对变量u的空间积分呢？COMSOL分享了积分耦合变量来实现这一功能
1.积分耦合变量分为四种：点(point)积分耦合变量、边(edge)积分耦合变量、边界(boundary)积分耦合变量、求解域(subdomain)积分耦合变量。根据模型的维度，会有相应积分耦合变量。用户还可以指定得到结果后的作用域，例如全局，或指定某些点、边、边界或求解域。从而可以将对积分耦合变量结果的访问限制在指定的对象上
2.求解域积分耦合变量，就是对指定变量或表达式在指定的某个或者某些求解域上做积分，积分的结果赋给自定义的这个积分耦合变量。对于三维仿真，这个积分是体积分；对于二维则是面积分。最典型的应用当属对数值1进行积分，可以得到体积或面积
3.边界积分耦合变量，就是对指定变量或表示在指定的某个或者某些边界上做积分，积分的结果付给自定义的这个积分耦合变量。对于三维仿真，这个积分是面积分；对于二维则是线积分。对1积分可以得到面积或边长
4.边积分耦合变量，就是对指定变量或表达式在指定的某个或者某些边上做积分，积分的结果付给自定义的这个积分耦合变量。仅存在于三维仿真中，这个积分是线积分。对1积分得到边长
5.点积分耦合变量，就是对指定变量或表达式在指定的某个或者某些点上给出它的值。它的最主要用法是将某个点上的结果映射到指定的对象上
6.在上面PID控制的例子中，指定位置处的浓度conc就是一个点积分耦合变量，用来提取点PT1处的浓度值。同时，浓度c的时间变化率ct在PT1点的取值，也可以用同样的方法提取出来，付给变量ctim
7.积分耦合变量除了用于添加约束，也常常用于后处理。COMSOL允许用户将任意表达式在任意求解域或者边界上的积分定义为一个变量，然后直接在后处理中对该自定义的积分耦合变量做数据可视化操作
8.例如，在二维扩散问题的仿真中，为了观测流出边界上总的流出的物质量，可以在出口边界利用边界耦合积分变量，然后可以直接得到数据曲线。（基本模块模型库 > Chemical engineering > absorption）
三、非线性特征值问题
1.求解方程的特征值是仿真中经常碰到的一类问题。问题线性度比较好的时候，方程的系数与方程的解变量u不存在函数关系，这样的方程很容易解；反过来，方程特征值也很容易求。但是有时候知识兔会碰到非线性比较强的问题，方程的系数本身就是解变量u的函数。对于正问题，COMSOL很容易“求解域设定”中，定义方程的某些系数是解变量的函数，然后利用COMSOL分享的非线性求解器完成求解。但是对于非线性很强的逆问题又该如何定义呢？这里有一个很好用的技巧，就是使用全局约束对特征值先进行一下归一化，在这里定义特征值与解变量相关。
2.例如PDE方程即为特征值（下图中的Lambda）。知识兔可以先添加全局约束，定义E=1，而E其实是一个积分耦合变量，对应于解变量u2在求解域上的积分。通过这样操作，知识兔就把Lambda和解变量u建立的联系，然后使用COMSOL分享的非线性求解器完成求解

comsol5.2新功能

知识兔1、多物理场
预定义多物理场耦合包括：焦耳热和热膨胀;电磁感应、微波、激光加热;热应力;热电和压电效应;非等温流;光电元件;等离子体热源;声-结构耦合;热声-结构和气动声学-结构耦合;多孔介质声学和多孔结构耦合
2、几何和网格
现在可以根据导入的网格构建几何，并可通过链接的子序列调用几何子序列，同时提升了大型阵列和CAD装配体的处理速度
3、优化和多功能
粒子追踪模块现包含粒子累积、侵蚀和刻蚀功能，且已加入多元分析优化模块
4、求解和求解器
本次更新中大幅优化了 CAD 装配体的模拟功能、支持额外维度、并支持对材料集和用户自定义函数进行扫描;同时改进了求解过程中的探针功能、支持参数化扫描以及在给定间隔内搜寻特征频率功能
5、材料与函数
可以对材料进行拷贝、粘贴、复制以及拖放等操作。当在不同的组件中使用相同材料时，可通过材料链接来链接到全局材料。
6、力学
使用结构力学模块模拟几何非线性梁、关节中非线性弹性材料和弹性材料功能。在传热模块中，可以模拟薄层、膜、裂隙和杆，以及低温破坏和平行辐射。声学模块新增了两个高频声波或几何声学的建模方法：射线声学和声扩散。
7、流体
支持在管道流模块中自动将管道连接到三维流动域， CFD 模块增加了两个新的代数湍流模型、并增加了湍流风扇和栅板。
8、电气
AC/DC 模块、RF 模块和波动光学模块都有了由频率和材料控制的自动网格剖分建议，因此可以方便地对无限元和周期性边界进行一键式网格剖分。等离子体模块分享了用于模拟平衡放电的接口
9、化工
化学反应工程模块包含了新的化学接口，可以用作化学反应的材料节点

软件特点

知识兔1、求解多场问题=求解方程组，用户只需选择或者自定义不同专业的偏微分方程进行任意组合便可轻松实现多物理场的直接耦合分析
2、完全开放的架构，用户可在图形界面中轻松自由定义所需的专业偏微分方程
3、任意独立函数控制的求解参数，材料属性、边界条件、载荷均支持参数控制
4、专业的计算模型库，内置各种常用的物理模型，用户可轻松选择并进行必要的修改
5、内嵌丰富的 CAD 建模工具，用户可直接在软件中进行二维和三维建模
6、全面的第三方 CAD 导入功能，支持当前主流CAD软件格式文件的导入
7、强大的网格剖分能力，支持多种网格剖分，支持移动网格功能
8、大规模计算能力，具备Linux、Unix 和Windows 系统下64 位处理能力和并行计算功能
9、丰富的后处理功能，可根据用户的需要进行各种数据、曲线、图片及动画的输出与分析
10、专业的在线帮助文档，用户可通过软件自带的操作手册轻松掌握软件的操作与应用
11、多国语言操作界面，易学易用，方便快捷的载荷条件，边界条件、求解参数设置界面

comsol命令集

知识兔一、 
comsol:启动COMSOL?
comsol?server:启动COMSOL?SERVER，用于联用MATLAB?
comsol?client:启动COMSOL?CLIENT?
comsol?batch:命令行模式的COMSOL，用于运行一个MPH算例或class文件?
comsol?compile:编译模型java文件，用于JAVA?API?
comsol?
server?matlab:启动MATLAB并连接到COMSOL?SERVER，SSH下个人推荐这种方式，原因自己体会?
comsol?matlab:启动MATLAB,并设置COMSOL的路径，不灵的(它没把mli下级目录添加进去，因此需要手动设置下)?
comsol?convertpre35a:转换COMSOL?v3.x版本模型，我觉得是生成高版本的MPH或M文件?
comsol?mph:运行COMSOL并行模式（multiprocessing?daemon）
二、
-h:屏显HELP?
?
-h:屏显的HELP?
-32:32位模式?
-64:64位模式?
-3drend?ogl|sw:OpenGL的3D渲染?
-np?:启动核数，WIN窗口模式默认启动全部核心，LIN则需要配置?
-numasets?:非一致性内存访问?(NUMA)硬件可以通过将专用内存与CPU配对来显著提高性能，通常为CPU核sockets数?
-mpmode?throughput|:并行模式?优化COMSOL与其他线程同时运行???????
turnaround|:并行模式?在无其他任务进行时，优化COMSOL进程????????????
owner:并行模式?在所有进程中，给予最高级的性能配置?
-blas?{auto}|?mkl|:basic?linear?algebra?operations，COMSOL很多计算引擎依赖BLAS?????????
acml|path:使用BLAS库?mkl:intel的CPU，acml：AMD?SSE2支持的CPU?
-blaspath?:BLAS库路径，与-blas?path联用（环境变量为LD_LIBRARY_PATH）?
-ipv6:IPV6支持?
-nn?:节点数?
-nnhost?:每个HOST使用的节点数?
-mpi?{auto}|intel|???
mpich2|wccs2003|?
whpc2008|user|path:调用MPI库?     
-mpipath?:MPI库路径?
-mpiroot?:MPI库root路径?
-mpirsh?{rsh}|ssh:在MPD模式下使用rsh或ssh?
-scalapack?{auto}|mpich2|wccs2003|whpc2008|user|path:Scalapcak库?
-scalapackpath?:Scalpack库路径?
-clusersimple:Simple?cluser模式???
-prefsdir?:配置属性路径?
-tmpdir?:临时文件路径?
-version:屏显版本号?
-ckl:使用class-kit?许可?
-forcegcc:强制加载GCC库，通常是在联用MATLAB，而函数无法返回MATLAB时使用?
-forcecomsolgcc:与COMSOL强制加载GCC库，COMSOL通常默认使用系统GCC，当在无法正常启动COMSOL时，尝试使用该命令
三、COMSOL SERVER命令 
通用格式  
comsol [] server []    
comsol target arguments
-user : login user name 
-port : TCP/IP port to listen  
-passwd : 当需要分享新密码时使用，如果不需要存储新密码联用nostore 
-login <{info}/force/never>: 查询登录信息 
-multi on | {off}: 允许client重复链接 
-silent: 不接受标准输入  
-graphics: 启动COMSOL的图形库，不在COMSOL的GUI下，但是是COMSOL的绘图模式

comsol常见问题解答

知识兔一、COMSOL绘图时出现显示错误的解决？
刚电脑上安装好comsol准备尝试新电脑是不是能正常使用这款软件进行分析。但是发现导入模型进行计算后得到的图像显示效果特备差，当时心里不好受啊，4k多的大洋就这破电脑。新买的电脑，虽然是i5低电压，但是显卡为950M，不至于显示会这么差啊，当时想到自己被坑了。后来不死心，我就各种百度，发现有人也有这个问题，经过耐心按照步骤来终于发觉，应该设置一下软件渲染，不然电脑显示的图像就像没有显卡一样
操作步骤:
1.打开COMSOL软件；
2.选择左上角文件选线，选择倒数第二项“首选项”
3.找图形和绘图窗口，可视化里面渲染选软件
4.渲染选项有3个，软件不行就选择其他，当时我一个个试，最终就能行了(选择后记得保存设置，设置后最好重启软件再试试)
二、comsol显示错误？
网格不够细，参数不符合真实物理条件，模型建立中有错误（公式部分），跟你的模型的几何结构也有关系。即便这些都没有问题，你所采用的求解器也会有很大的影响。举个例子，我求解过一个稳态问题，是多场耦合的。如果我用segregated solver，总是无法收敛，但是如果我用fully coupled solver，却可以收敛。还有一个能想到的原因就是，你的初始值的设置，越符合真实物理情况越好，越接近最终解越好（看你猜的本领了）。调试时建议先从一个简单的可行的model开始
三、为何产生网格与后处理时，有时图形无法正确显示？
这是由于显卡不支持硬件加速 OpenGL1.1或更新版本造成的，解决办法为在桌面单击右键——属性——设置——高级——疑难解答——硬件加速，将其关闭。使用软件来加速，可以解决问题。第二种办法是更换支持 OpenGL1.1或更新
四、如何增加内存使用量？
1.使用最新版本的软件，因为随着软件版本的升级，对于内存的控制也越来越好，可以使用小内存计算大规模问题，且不会影响计算速度。
2.至 COMSOL 3.2 文件夹 lib，打开文件 comsol.opts，将其中一行“MAXHEAP=256m”， 从256MB调至128MB或更低
五、如何避免高度非线性的不收敛问题？
1.PDE 形式使用 general solution form 或是 weak solution form，会大大提高收敛性。此外，当使用到耦合变量时，必须使用 weak solution form 来得到准确的 Jacobian。
2.使用最有可能的初始值
3.确保边界条件一致性
4.将稳态非线性问题切换成瞬时问题并试着去求解
5.使用参数解，以及变化与非线性行为很大关系的材料系数，因此可以一连串的微调方程式的非线性程度
六、如何避免几何结构奇点
几何奇点是指尖锐的角或是在网格化、分析过程中产生问题的角，尖锐的角在结构问题分析会导致无限大的应力值。为了避免奇异点，可以使用绘图模式下的圆角(Fillet) 绘图指令在模型的角边产生一个圆角，使其应力值有限

特别说明

百度网盘提取码：6r5h

下载体验

 

点击下载